| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- RS-485
- 퀄컴
- 힐스테이트 광교산
- ConnectedHomeIP
- Apple
- 애플
- Espressif
- 코스피
- 국내주식
- 오블완
- 파이썬
- 취미생활
- 나스닥
- 배당
- 미국주식
- 해외주식
- 월패드
- 티스토리챌린지
- 매터
- 엔비디아
- 홈네트워크
- matter
- Home Assistant
- raspberry pi
- Bestin
- Python
- homebridge
- esp32
- MQTT
- 현대통신
- Today
- Total
YOGYUI
Confusion Matrix (혼동행렬) 본문
지난주 토요일(4/17) 빅데이터분석기사 필기시험을 치렀다
데이터분석전문가(ADP)를 딴지 얼마 안돼서 그런지 체감 난이도는 그저 그런 수준? (어차피 출제기관은 한국데이터산업진흥원으로 동일하다)
특이한건, 전체 80문제 중에 confusion matrix 관련 문제가 내 기억에 따르면 3문제나 나왔다는 점이다 (ROC 커브 포함)
아무래도 단순 계산 문제로도 내기 좋고 개념 문제로 내기도 좋다보니 출제 비중이 높은 것 같다
(특히 metric 개념은 공부 안해가면 찍는거 말곤 할 수 있는게 없다)
앞으로도 ADP나 분석기사 모두 필기시험에서는 최소 1문제 이상은 무조건 출제될 것 같으니 블로그에 한 번 정리해보자
혼동행렬(Confusion Matrix)는 (특히 이진 분류 문제) 데이터 분석 모델의 예측 결과와 실제 데이터를 행렬 형태로 다음과 같이 나타낸 것이다
※ 편의를 위해 데이터는 0과 1로 분류된다고 하자

행렬의 각 요소별 명칭은 직관적이다
- 분석 모델이 1로 예측하면 Positive, 0으로 분류하면 Negative
- 분석 모델의 예측 결과가 실제 데이터랑 동일하면 (제대로 예측한 경우) True, 틀렸으면 False
- 분석 모델이 1로 예측했는데 실제 데이터도 1인 경우 True Positive (TP, 참긍정)
- 분석 모델이 1로 예측했는데 실제 데이터는 0인 경우 False Positive (FP, 거짓긍정)
- 분석 모델이 0으로 예측했는데 실제 데이터는 1인 경우 False Negative (FN, 거짓부정)
- 분석 모델이 0으로 예측했는데 실제 데이터도 0인 경우 True Negative (TN, 참부정)
이제 혼동행렬에서 바로 계산할 수 있는 5가지 메트릭들을 알아보자
- Precision (정밀도)
모델이 1로 예측한 결과 중 실제 데이터도 1인 경우의 비율: TPTP+FP
'모델'의 관점

- Recall (재현율)
실제 값이 1인 데이터 중 모델이 1로 예측한 비율: TPTP+FN
'데이터'의 관점
= Sensitivity (민감도) = TPR (True Positive Rate) = Hit Rate

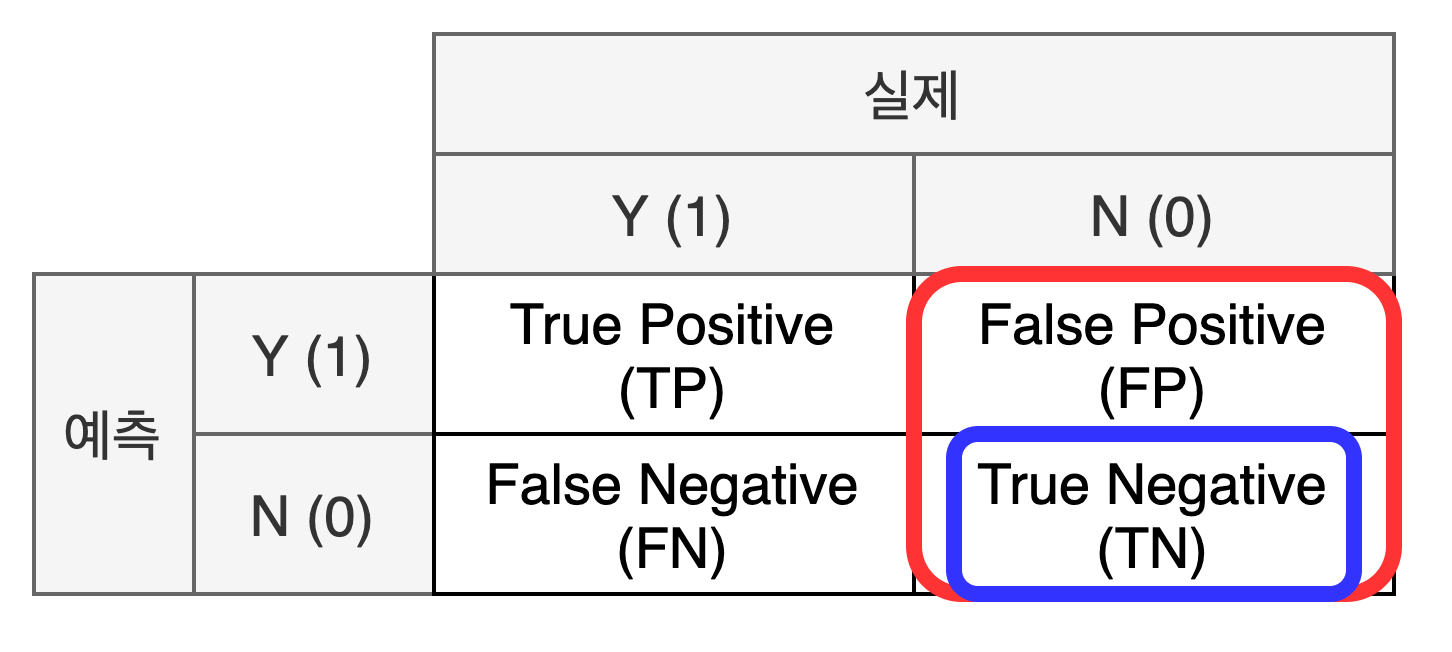
- Specificity (특이도)
실제 값이 0인 데이터 중 모델이 0으로 예측한 비율: TNFP+TN
'데이터'의 관점
= TNR (True Negative Rate)
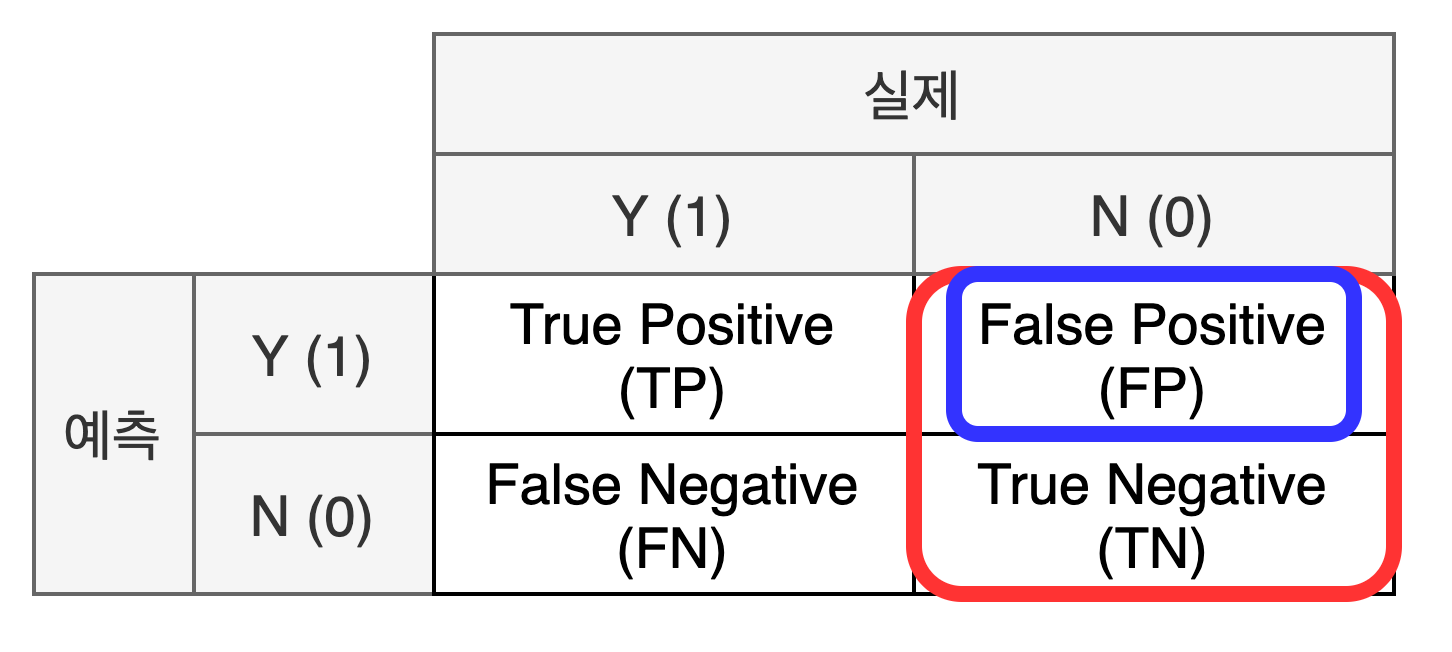
- False Positive Rate (FPR, 거짓긍정률)
실제 값이 0인 데이터 중 모델이 1로 잘못 예측한 비율: FPFP+TN=1−Specificity
'데이터'의 관점
- Accuracy (정확도)
모델이 제대로 예측한 비율: TP+TNTP+FP+FN+TN

정밀도나 정확도는 이름이 유사해서 헷갈릴 수는 있지만 모델의 관점에서 계산한다는 점에서 용어는 직관적이다
그런데 재현율이나 민감도는 아무래도 개념이 낯설다보니 억지로 외워줘야 한다
대충 검색해보니 의학통계 쪽에서 주로 쓰는 용어인 듯하다 (치료에 따른 질병의 재발율 뭐 이런 느낌으로 쓰는 듯?)
위 5개 기본 메트릭은 혼동행렬을 구한 뒤 바로 계산 가능한 값들이고 다음 2개 메트릭은 기본 메트릭들을 활용해서 계산할 수 있다
- F1 Score (F-Measure)
정밀도와 재현율의 조화평균: 21precision+1recall=2×TP2×TP+FP+FN
모델의 예측 성능을 수치화, 값의 범위는 0 ~ 1
정밀도 혹은 재현율 둘 중 하나만 높은 경우보다 정밀도와 재현율 둘 다 값이 클 경우 F1 점수는 1에 가까워진다 = 모델의 예측 성능이 좋다
※ F1-score까지는 이해를 하던 암기를 하던 필기시험 칠때는 무조건 머리에 집어넣자
- Kappa Value (Kappa Statistics, 카파값)
κ=P(a)−P(e)1−P(e)
P(a)=accuracy
P(e)=(TP+FP)×(TP+FN)×(FN+TN)×(FP+TN)(TP+FP+FN+TN)2
모델의 예측 결과와 실제 데이터가 '우연히' 일치할 확률을 제외한 뒤 매기는 점수, 값의 범위는 0 ~ 1
1에 가까울수록 예측값과 실제값이 일치
[참고도서]
권재명, 『실리콘밸리 데이터과학자가 알려주는 따라하며 배우는 데이터과학』, 제이펍(2017)
서민구, 『R을 이용한 데이터 처리 & 분석 실무』, 길벗(2014)
정혜정·장희선, 『빅데이터분석기사 한권으로 끝내기』, 시대고시기획(2020)
'Data Analysis > General' 카테고리의 다른 글
| 자연상수 (오일러 수) e 값 구해보기 (0) | 2021.12.10 |
|---|---|
| Mean Value Theorem(평균값 정리) - 구간 단속카메라 원리 (2) | 2021.10.07 |
| Benford's Law (벤포드의 법칙) (0) | 2021.02.23 |




