| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- matter
- homebridge
- 나스닥
- 힐스테이트 광교산
- 티스토리챌린지
- 해외주식
- 엔비디아
- 미국주식
- 취미생활
- 오블완
- esp32
- MQTT
- 배당
- Home Assistant
- RS-485
- 홈네트워크
- raspberry pi
- 퀄컴
- Apple
- 국내주식
- 코스피
- ConnectedHomeIP
- Python
- 애플
- 현대통신
- Espressif
- 월패드
- Bestin
- 매터
- 파이썬
- Today
- Total
YOGYUI
Mean Value Theorem(평균값 정리) - 구간 단속카메라 원리 본문

2주 전쯤에 서점에 놀러갔다가 책 하나를 발견해서 심심풀이삼아 샀다
한화택, 『미적분의 쓸모』, 더퀘스트(2021)
순간 속도(가속도), 인공지능과 빅데이터(최적화), CT촬영(기하학), 나비에-스토크스 유동방정식, 한계효용 등 여러가지 일상 생활 속 여러 사례에서 미분과 적분이 활용되는 사례들을 다루고 있는데, 디테일한 수식이나 증명과정은 거의 나오지 않아 물 흘러가듯이 쓰윽 완독할만하다 (2시간정도 걸린 것 같다)
이 중, 본문 1장 '혁명의 시작, 순간 속도를 계산하라'에 평균값 정리와 이를 활용한 자동차 과속 단속카메라의 원리에 대한 내용이 있어 간단하게 소개해보고자 한다
평균값 정리(Mean Value Theorem, MVT)
고등학교에서 이과를 선택했다면 한번쯤은 들어봤을 이론...이겠지? ㅋㅋ
함수 f(x)가
(1) 닫힌 구간 [a,b]에서 연속이고
(2) 열린 구간 (a,b)에서 미분 가능할 때
f′(c)=f(b)−f(a)b−a
를 만족하는 c가 구간 (a,b)에 최소 하나 이상 존재한다
말로 풀어쓰면
구간에서의 평균 변화율과 같은 순간 변화율을 갖는 지점이 1개 이상 존재한다
곡선이 두 끝점을 잇는 선과 평행하는 접선을 가진다
그림으로 간단하게 표시해보면

증명
평균값 정리의 증명에는 롤의 정리(Rolle's theorem)가 사용된다
함수 f(x)가
(1) 닫힌 구간 [a,b]에서 연속이고
(2) 열린 구간 (a,b)에서 미분 가능하고
(3) f(a)=f(b)일 때
f′(c)=0이 되는 c가 구간 (a,b) 사이에 최소 하나 이상 존재한다
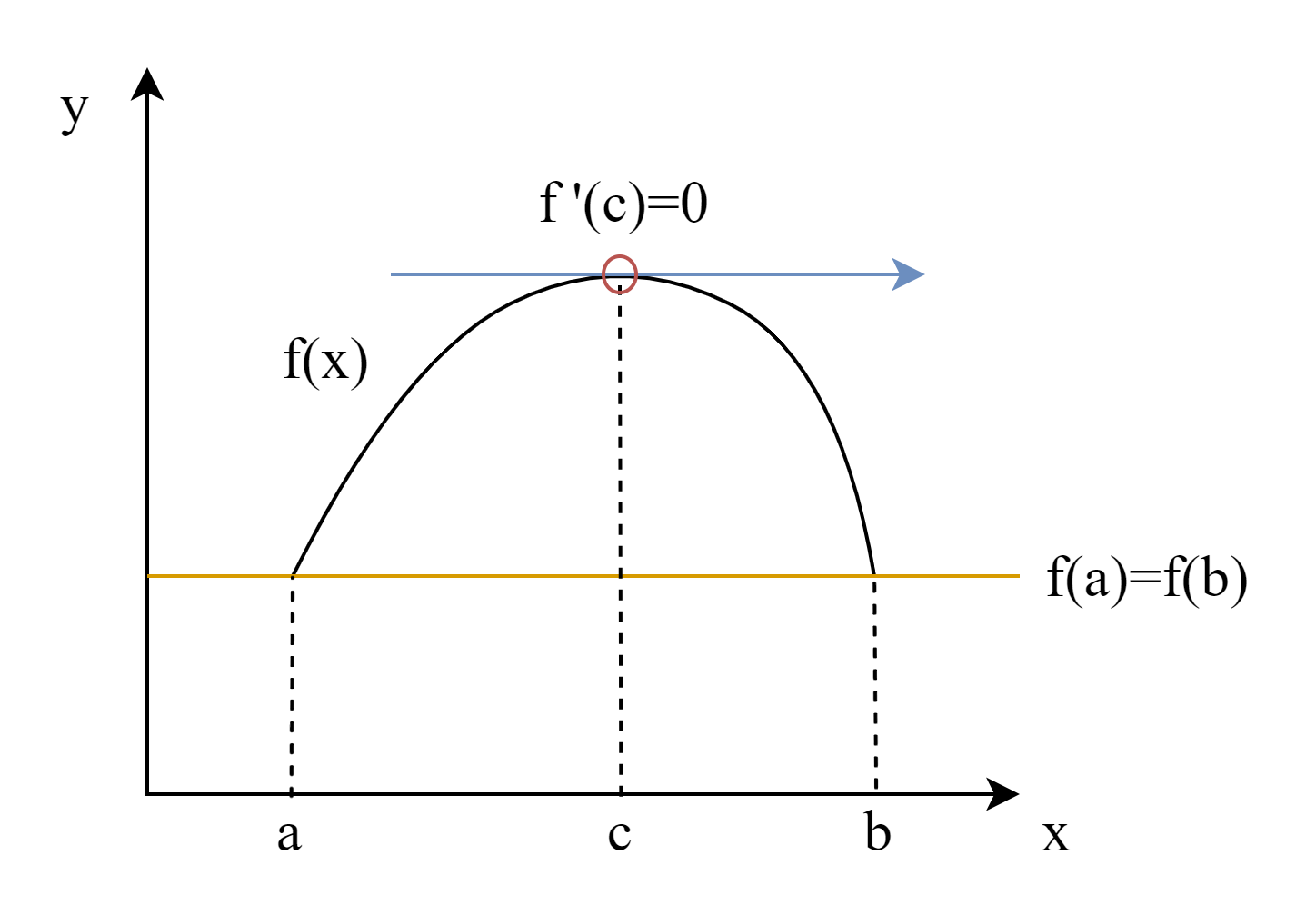
결국 평균값 정리에서 f(a)=f(b)인 특수한 경우를 다룬 것이 롤의 정리라 할 수 있다
롤의 정리의 증명은 굳이 여기서 다루진 말자...
이제 평균값 정리를 증명해보자
곡선의 양 끝점을 통과하는 직선 g(x)는 다음과 같다
g(x)=f(b)−f(a)b−a(x−a)+f(a)
원함수 f(x)에서 직선g(x)을 뺀 함수를 h(x)라 하자
h(x)=f(x)−g(x)=f(x)−(f(b)−f(a)b−a(x−a)+f(a))
함수 h(x)는 h(a)=h(b)=0이므로 롤의 정리를 만족시킨다
따라서 h′(c)=0이 되는 c가 (a,b)에 최소 하나 이상 존재하게 되는데,
h′(c)=f′(c)−g′(c)=f′(c)−f(b)−f(a)b−a=0
즉 f′(c)=f(b)−f(a)b−a을 만족시키는 c가 (a,b) 구간 내에 적어도 하나 존재한다
자동차 과속 구간 단속카메라
이제는 운전하다보면 '구간단속시점' 도로교통표지판을 흔히 볼 수 있다

구간 과속 카메라는 (일반적으로) 3차례 과속 여부 측정을 하게 된다
- 구간 시작점 과속여부 (고정식)
- 구간 끝점 과속여부 (고정식)
- 구간 평균속도 과속여부
※ 3차례 모두 과속 측정되었더라도 벌금 부과는 한 번만 한다고 한다
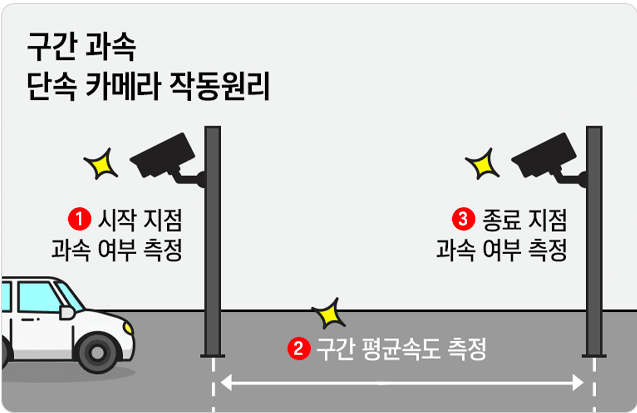
이 때, 3번째 '구간 평균속도 과속여부' 판단 시 평균값 정리가 사용되는 것이다
이동 거리를 시간에 대해 미분하면 속도가 된다
(엄밀히 말하면 물리학적으로는 '속력'이지만... 일상 생활에서는 스칼라와 벡터를 굳이 구분해서 쓰지는 않으니...)
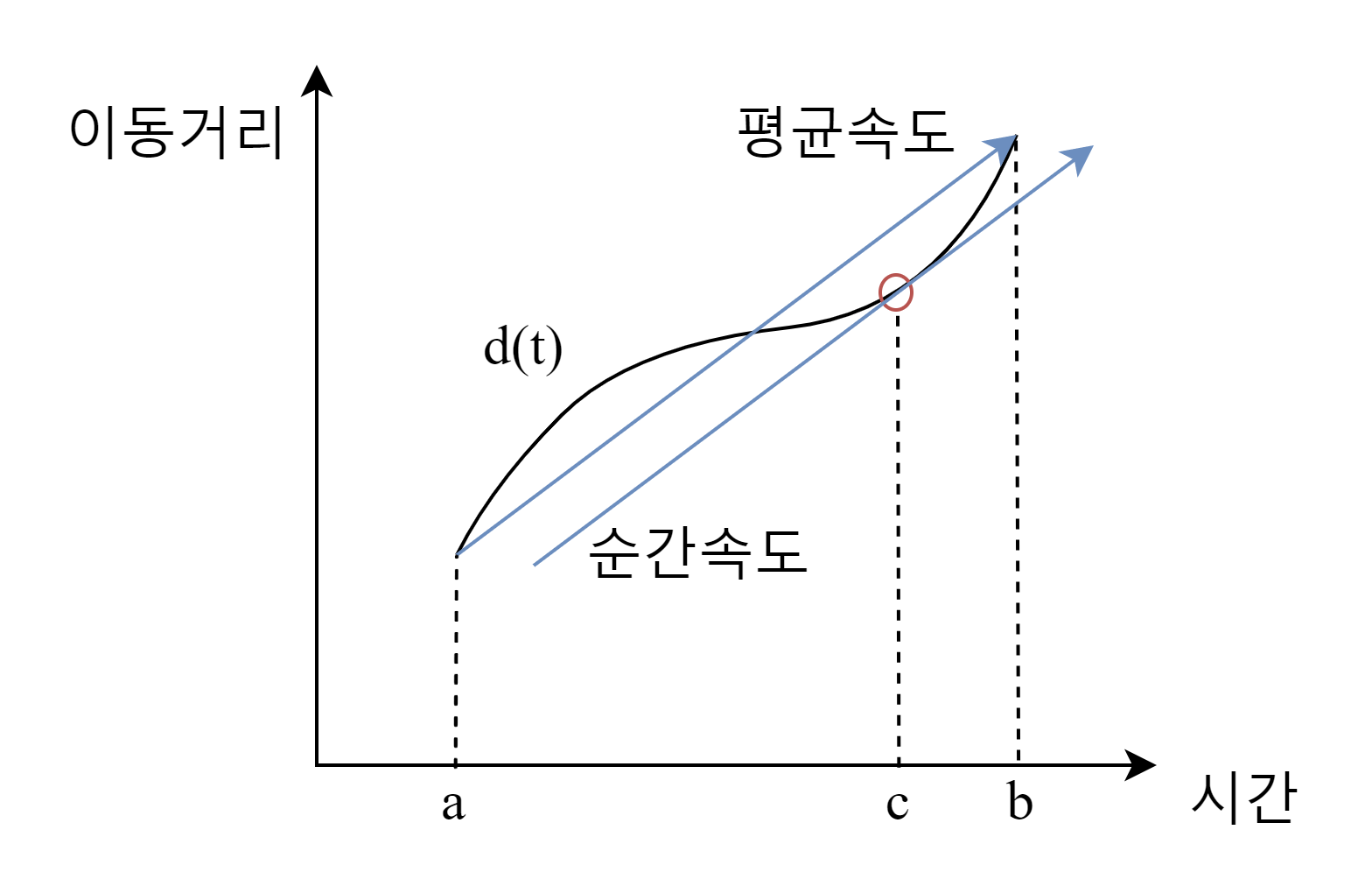
다시 말해 단속 구간을 통과한 후 전체 평균 속도가 규정 속도를 넘었다면 구간 내에서 적어도 한 번은 규정 속도를 넘었다고 봐야 한다. 그러니 "전체 구간에서 평균 속도는 규정 속도를 넘었을지언정 중간에 규정 속도를 넘은 적이 한 번도 없다"고 우기면 안 된다. (책 39페이지)
시작 지점과 끝 지점의 속도는 캥거루 운전을 통해서 피할 수 있지만 평균 속도는 어찌 피할 방법이 없다. 초반에 빨리 달린 적이 있다면 단속 종료 지점에 너무 일찍 도달하지 않기 위해 중간에 어디선가 시간을 보내야 한다. 휴게소라도 있으면 좋으련만 단속 구간 사이에 휴게소가 있는 경우는 거의 없다. 그러니 처음에는 빨리 달리다가도 나중에 천천히 달릴 수 밖에 없는 구조다. 조급한 마음을 버리고 여유 있게 운전하는 것이 정답이다. (책 40페이지)
그러니, 구간 단속 지점에서 단속된 뒤에 괜히 우길 생각하지 말고 규정 속도에 맞춰서 운행하는 게 정신건강에 이롭다~
(요새 출시되는 차들은 레벨1 자율주행 - 크루즈컨트롤이 왠만하면 기본 옵션으로 탑재되어 있으니 적극 활용하면 운전 피로도도 많이 줄고 단속에 걸릴 일도 없다)
책에서는 이 외에도 도플러 효과를 이용한 이동식 단속카메라, 영상처리기법을 이용한 단속카메라 등에 대한 내용도 간단하게 다루고 있다
끝~!
[출처]
https://ko.wikipedia.org/wiki/%ED%8F%89%EA%B7%A0%EA%B0%92_%EC%A0%95%EB%A6%AC
https://ko.wikipedia.org/wiki/%EB%A1%A4%EC%9D%98_%EC%A0%95%EB%A6%AC
https://j1w2k3.tistory.com/359
https://m.blog.naver.com/davidj09/220999129207
'Data Analysis > General' 카테고리의 다른 글
| 자연상수 (오일러 수) e 값 구해보기 (0) | 2021.12.10 |
|---|---|
| Confusion Matrix (혼동행렬) (0) | 2021.04.25 |
| Benford's Law (벤포드의 법칙) (0) | 2021.02.23 |



