| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
- RS-485
- homebridge
- Home Assistant
- 마이크로소프트
- 배당
- Espressif
- 월패드
- 나스닥
- 홈네트워크
- 힐스테이트 광교산
- Python
- 코스피
- 공모주
- MQTT
- 오블완
- matter
- 애플
- 미국주식
- raspberry pi
- esp32
- 해외주식
- 매터
- Apple
- Bestin
- ConnectedHomeIP
- 파이썬
- 국내주식
- 티스토리챌린지
- 현대통신
- 라즈베리파이
- Today
- Total
YOGYUI
R 회귀분석 모델 성능판단 - RMSE, MAE, R squared 본문

분류분석(Classification)은 모델의 분류 성능을 판단할 때 모델의 class 분류 결과에 따라 Confusion Matrix를 작성하고 ROC, AUC 등을 metric을 활용한다
반면 회귀분석(Regression)은 출력이 수치형 데이터이므로 실제 학습 대상값과의 '차이'를 기반으로 모델의 성능을 판단하는게 일반적인데, 이 때 많이 쓰이는 metric이 RMSE, MAE, R squared (결정계수) 값이다
- 결정계수는 모델이 학습 데이터에 얼마나 잘 fitting 되었는지를 판별하는 용도로 사용
RMSE=√1N∑Ni=1(yi−^yi)2
MAE=1N∑Ni=1|yi−^yi|
R2=(∑Ni=1(yi−ˉy)(^yi−ˉˆy)√∑Ni=1(yi−ˉy)2√∑Ni=1(^yi−ˉˆy)2)2
R2adjusted=1−(n−1)(1−R2)n−p−1
y: 데이터 실제값
ˆy: 모델의 예측값
n: 데이터 레코드 수
p: 데이터의 변수(속성) 개수
R에서는 RMSE나 MAE 계산은 수식 한줄로 구현 가능하기 때문에 패키지를 굳이 쓸 필요없이 함수로 작성하는게 간단하다
R squared는 lm이나 glm 모델은 자동으로 계산되어 summary를 통해 확인할 수 있다
rmse <- function(y1, y2) {
sqrt(mean((y1 - y2) ^ 2))
}
mae <- function(y1, y2) {
mean(abs(y1 - y2))
}
rsquare <- function(y1, y2) {
sum((y1 - mean(y1)) * (y2 - mean(y2))) ^ 2 / (sum((y1 - mean(y1)) ^ 2) * sum((y2 - mean(y2)) ^ 2))
}
rsquare_adj <- function(y1, y2, p) {
n <- length(y1)
rsq <- rsqare(y1, y2)
1 - (n - 1) * (1 - rsq) / (n - p - 1)
}각각이 어떤 의미를 갖고 있는지는 굳이 여기서 설명하지 않기로 한다
Example
실습삼아 보스턴 주택 가격 데이터로 회귀모델을 학습한 후 학습데이터 및 검증데이터에서의 RMSE와 MAE를 구해보고 학습모델의 R Squared값도 구해보자
(홀드아웃은 Train - Test 2 세트로만 진행, 데이터전처리 제외)
library(mlbench)
data(BostonHousing)
# Hold out
library(caret)
idx <- caret::createDataPartition(BostonHousing$medv, p = 0.8)
df_train <- BostonHousing[idx$Resample1, ]
df_test <- BostonHousing[-idx$Resample1, ]
# linear regression model
model_lm <- lm(medv ~ ., data = df_train)
y_pred_train_lm <- predict(model_lm, newdata = df_train)
rsq_train_lm <- rsquare(y_pred_train_lm, df_train$medv)
rsq_adj_train_lm <- rsquare_adj(y_pred_train_lm, df_train$medv, length(model_lm$coefficients) - 1)
y_pred_test_lm <- predict(model_lm, newdata = df_test)
rmse_test_lm <- rmse(y_pred_test_lm, df_test$medv)
mae_test_lm <- mae(y_pred_test_lm, df_test$medv)rmse_test_lm
> [1] 4.899621
mae_test_lm
> [1] 3.098167
rsq_train_lm
> [1] 0.7441116
rsq_adj_train_lm
> [1] 0.7356471summary(model_lm)
>
Call:
lm(formula = medv ~ ., data = df_train)
Residuals:
Min 1Q Median 3Q Max
-15.9815 -2.7418 -0.6664 2.0214 25.6129
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 32.848254 5.571636 5.896 8.04e-09 ***
crim -0.105552 0.034080 -3.097 0.002094 **
zn 0.047434 0.014757 3.214 0.001415 **
indus 0.018797 0.069091 0.272 0.785721
chas1 2.841013 0.900571 3.155 0.001730 **
nox -15.885153 4.223124 -3.761 0.000195 ***
rm 4.058418 0.463493 8.756 < 2e-16 ***
age -0.009839 0.015178 -0.648 0.517224
dis -1.505226 0.221435 -6.798 3.96e-11 ***
rad 0.261729 0.070931 3.690 0.000256 ***
tax -0.011529 0.004063 -2.838 0.004781 **
ptratio -0.864258 0.144621 -5.976 5.13e-09 ***
b 0.008748 0.003119 2.805 0.005288 **
lstat -0.486404 0.055553 -8.756 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.717 on 393 degrees of freedom
Multiple R-squared: 0.7441, Adjusted R-squared: 0.7356
F-statistic: 87.91 on 13 and 393 DF, p-value: < 2.2e-16summary에 나오는 'R-squared'와 'Adjusted R-squared' 값이 함수로 직접 구현한 값과 같은 것을 확인
변수간 교호작용을 고려한 모델링 후 MASS 패키지를 이용해서 변수선택까지 진행해보자 (후진제거법)
library(MASS)
model_lm2 <- lm(medv ~ .^2, data = df_train)
model_lm2_step <- MASS::stepAIC(model_lm2, scope = list(upper = ~ .^2, lower = ~-1))
y_pred_train_lm2 <- predict(model_lm2_step, newdata = df_train)
rsq_train_lm2 <- rsquare(y_pred_train_lm2, df_train$medv)
rsq_adj_train_lm2 <- rsquare_adj(y_pred_train_lm2, df_train$medv, length(model_lm2_step$coefficients) - 1)
y_pred_test_lm2 <- predict(model_lm2_step, newdata = df_test)
rmse_test_lm2 <- rmse(y_pred_test_lm2, df_test$medv)
mae_test_lm2 <- mae(y_pred_test_lm2, df_test$medv)summary(model_lm2_step)
>
Call:
lm(formula = medv ~ crim + zn + indus + chas + nox + rm + age +
dis + rad + tax + ptratio + b + lstat + crim:zn + crim:chas +
crim:nox + crim:rm + crim:rad + crim:tax + crim:ptratio +
crim:b + crim:lstat + zn:tax + zn:lstat + indus:nox + indus:rm +
indus:dis + indus:ptratio + indus:b + chas:nox + chas:rm +
chas:tax + chas:ptratio + chas:lstat + nox:age + nox:b +
nox:lstat + rm:age + rm:tax + rm:ptratio + rm:lstat + age:dis +
age:rad + age:tax + age:ptratio + age:b + age:lstat + dis:tax +
dis:lstat + rad:lstat + tax:ptratio + tax:b + tax:lstat,
data = df_train)
Residuals:
Min 1Q Median 3Q Max
-7.0778 -1.6094 -0.1441 1.2811 20.3616
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.671e+02 2.493e+01 -6.702 8.14e-11 ***
crim -9.895e+00 5.265e+00 -1.879 0.061000 .
zn -9.446e-02 3.902e-02 -2.421 0.015982 *
indus -2.657e+00 1.145e+00 -2.322 0.020817 *
chas1 7.567e+01 1.386e+01 5.461 8.93e-08 ***
nox 2.333e+01 1.941e+01 1.202 0.230128
rm 2.943e+01 2.519e+00 11.685 < 2e-16 ***
age 1.234e+00 2.333e-01 5.289 2.17e-07 ***
dis 5.218e-01 5.864e-01 0.890 0.374200
rad -2.720e-01 2.052e-01 -1.325 0.185868
tax 9.096e-02 4.477e-02 2.032 0.042931 *
ptratio 1.874e+00 1.182e+00 1.586 0.113623
b 7.360e-02 2.646e-02 2.781 0.005704 **
lstat 1.458e+00 4.701e-01 3.101 0.002085 **
crim:zn 2.562e-01 1.210e-01 2.116 0.035015 *
crim:chas1 1.881e+00 5.429e-01 3.464 0.000598 ***
crim:nox -2.606e+00 7.491e-01 -3.479 0.000567 ***
crim:rm 2.066e-01 4.422e-02 4.673 4.24e-06 ***
crim:rad -3.751e-01 1.672e-01 -2.244 0.025453 *
crim:tax 1.681e-02 9.972e-03 1.686 0.092765 .
crim:ptratio 3.698e-01 2.231e-01 1.658 0.098270 .
crim:b -2.086e-04 1.432e-04 -1.457 0.146090
crim:lstat 3.117e-02 5.499e-03 5.669 2.99e-08 ***
zn:tax 5.104e-04 1.374e-04 3.714 0.000237 ***
zn:lstat -1.031e-02 2.779e-03 -3.710 0.000240 ***
indus:nox 1.695e+00 8.006e-01 2.117 0.034947 *
indus:rm 3.607e-01 8.942e-02 4.034 6.74e-05 ***
indus:dis -7.471e-02 4.209e-02 -1.775 0.076760 .
indus:ptratio -5.264e-02 2.736e-02 -1.924 0.055195 .
indus:b 2.027e-03 1.373e-03 1.476 0.140855
chas1:nox -4.373e+01 1.069e+01 -4.090 5.35e-05 ***
chas1:rm -6.388e+00 1.064e+00 -6.003 4.82e-09 ***
chas1:tax 1.874e-02 1.369e-02 1.369 0.171886
chas1:ptratio -8.674e-01 5.323e-01 -1.630 0.104095
chas1:lstat -2.590e-01 1.460e-01 -1.774 0.076907 .
nox:age -6.855e-01 2.029e-01 -3.378 0.000811 ***
nox:b -4.515e-02 3.369e-02 -1.340 0.181085
nox:lstat 1.153e+00 4.818e-01 2.393 0.017252 *
rm:age -6.514e-02 1.648e-02 -3.953 9.34e-05 ***
rm:tax -2.583e-02 3.721e-03 -6.940 1.88e-11 ***
rm:ptratio -5.386e-01 1.481e-01 -3.637 0.000316 ***
rm:lstat -2.609e-01 4.212e-02 -6.194 1.63e-09 ***
age:dis -1.572e-02 6.871e-03 -2.288 0.022749 *
age:rad 1.169e-02 2.947e-03 3.966 8.84e-05 ***
age:tax -2.738e-04 1.567e-04 -1.747 0.081530 .
age:ptratio -1.173e-02 5.100e-03 -2.301 0.021999 *
age:b -4.815e-04 2.095e-04 -2.299 0.022100 *
age:lstat -5.804e-03 1.733e-03 -3.350 0.000897 ***
dis:tax -4.408e-03 1.636e-03 -2.694 0.007391 **
dis:lstat 1.017e-01 3.598e-02 2.826 0.004978 **
rad:lstat -2.592e-02 8.784e-03 -2.951 0.003379 **
tax:ptratio 6.388e-03 1.745e-03 3.661 0.000290 ***
tax:b -4.841e-05 2.797e-05 -1.731 0.084390 .
tax:lstat -1.329e-03 5.326e-04 -2.495 0.013052 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.804 on 353 degrees of freedom
Multiple R-squared: 0.9188, Adjusted R-squared: 0.9066
F-statistic: 75.35 on 53 and 353 DF, p-value: < 2.2e-16length(model_lm2$coefficients)
> [1] 92
length(model_lm2_step$coefficients)
> [1] 54교호작용 적용 고려 모델의 총 92개 변수 중에서 54개가 선택되었다
rsq_train_lm2
> [1] 0.9187851
rsq_adj_train_lm2
> [1] 0.9065913
rmse_test_lm2
> [1] 3.069706
mae_test_lm2
> [1] 2.26649훈련 데이터 피팅 및 테스트 데이터 예측력 모두 향상된 것을 알 수 있다
의사결정나무와 랜덤포레스트 모델도 학습해보자
library(rpart)
model_tree <- rpart(medv ~ ., data = df_train)
y_pred_train_tree <- predict(model_tree, newdata = df_train)
rsq_train_tree <- rsqare(y_pred_train_tree, df_train$medv)
rsq_adj_train_tree <- rsqare_adj(y_pred_train_tree, df_train$medv, 13)
y_pred_test_tree <- predict(model_tree, newdata = df_test)
rmse_test_tree <- rmse(y_pred_test_tree, df_test$medv)
mae_test_tree <- mae(y_pred_test_tree, df_test$medv)
library(randomForest)
model_rf <- randomForest(medv ~ ., data = df_train)
y_pred_train_rf <- predict(model_rf, newdata = df_train)
rsq_train_rf <- rsqare(y_pred_train_rf, df_train$medv)
rsq_adj_train_rf <- rsqare_adj(y_pred_train_rf, df_train$medv, 13)
y_pred_test_rf <- predict(model_rf, newdata = df_test)
rmse_test_rf <- rmse(y_pred_test_rf, df_test$medv)
mae_test_rf <- mae(y_pred_test_rf, df_test$medv)
opar <- par(mfrow = c(1, 1), xpd = NA)
plot(model_tree)
text(model_tree, use.n = TRUE)
par(opar)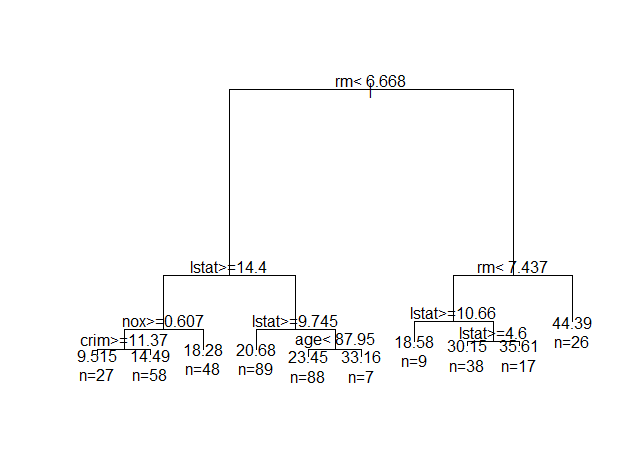
4개 모델 상호비교를 위해 데이터프레임 한개를 만들자
model_name <- c('LM', 'LM2', 'TREE', 'RF')
rsq <- c(rsq_train_lm, rsq_train_lm2, rsq_train_tree, rsq_train_rf)
rsq_adj <- c(rsq_adj_train_lm, rsq_adj_train_lm2, rsq_adj_train_tree, rsq_adj_train_rf)
rmse <- c(rmse_test_lm, rmse_test_lm2, rmse_test_tree, rmse_test_rf)
mae <- c(mae_test_lm, mae_test_lm2, mae_test_tree, mae_test_rf)result
>
model_name rsq rsq_adj rmse mae
1 LM 0.7441116 0.7356471 4.899621 3.098167
2 LM2 0.9187851 0.9065913 3.069706 2.266490
3 TREE 0.8203062 0.8143621 4.486154 3.308212
4 RF 0.9779394 0.9772097 3.202202 2.155022훈련용 데이터에 가장 잘 적합된 (혹은 과적합된) 모델은 random forest이며, 훈련되지 않은 데이터 (테스트 데이터)의 실제값에 가장 근접하게 예측하는 모델은 RMSE 기준으로는 교호작용 고려 모델링 후 변수선택한 모델 (lm2)이고 MAE 기준으로는 random forest이다
테스트 데이터의 실제값과 모델 예측값의 차이 여부는 상관관계(correlation)로도 나타낼 수 있다
cor 함수로 피어슨 상관계수를 모델별로 계산해보자
cor(y_pred_test_lm, df_test$medv)
> [1] 0.8517357
cor(y_pred_test_lm2, df_test$medv)
> [1] 0.9455954
cor(y_pred_test_tree, df_test$medv)
> [1] 0.8831279
cor(y_pred_test_rf, df_test$medv)
> [1] 0.9473627구현해 본 모델 중 random forest가 학습 결과 및 예측 정확도가 가장 우수한 것으로 나타났다
아웃라이어 제거, 정규화 및 표준화, 파생변수 생성 등 데이터 가공 시 성능은 더 올릴 수 있을 것 같으니 나중에 시간이 나면 해봐야겠다
'Software > R' 카테고리의 다른 글
| R caret::confusionMatrix - 혼동행렬 작성 및 metric 추출 (2) | 2021.06.17 |
|---|---|
| R caret::preProcess - 수치형 데이터 정규화, 표준화 (0) | 2021.06.17 |
| R pROC 패키지::ROC 커브 그리기, AUC 메트릭 계산하기 (0) | 2021.06.15 |
| R NA 처리하기 (with dplyr) (0) | 2021.06.13 |
| R 스크립트 파일 경로 가져오기 (0) | 2021.06.05 |




